I’ve tried to describe this project thoroughly, but if you have questions please leave a comment below and I’ll try to answer them.
Introduction
Setting circles on an astronomical telescope are used as an aid to pointing the telescope at a particular object in the sky based upon the object’s celestial coordinates. However, setting circles can be difficult to use effectively and are usually not precise enough for putting objects in the telescope’s field of view. Digital setting circles, on the other hand, can be made to be much more precise and fairly easy to use, making it relatively simple to find faint fuzzies in the sky without lots of star hopping.
What are digital setting circles? You’ve probably seen them in ads in the astronomy magazines: NGC MAX, Sky Wizard, and Sky Vector, to name a few. They’re hand-held electronic devices which, when coupled with encoders which precisely measure the movement of the telescope on its axes, can tell you precisely where your telescope is pointed, or can guide you directly to an object you specify. (It’s worth noting that digital setting circles do not move your telescope. Rather, they simply give you feedback as you move it yourself.) Some digital setting circles systems interface to a PC and can be controlled by software. TheSky, Megastar, and Earth Centered Universe are examples of commercial PC software which can communicate with digital setting circles systems. All of these packages integrate a planetarium view with the system and can be quite useful on portable computers used with the telescope in the field.
The project which I describe below is simply an interface between the encoders mounted on the telescope and a PC running appropriate control software. It is not a stand-alone unit–it is useless without a PC to communicate with it. It is compatible with several other types of digital setting circle interfaces, including BBox, NGC-MAX, SGT-MAX, and MicroGuider III. This compatibility means that the interface described below will work with many commercial software packages. My design is simple, inexpensive, and easy to build.
I’ve worked hard to document this design so that you can build it yourself. The parts are readily available and construction is straightforward. There is nothing terribly challenging in building this device. If you have some experience with building electronic kits, you can build this interface with no problem. If you don’t, find someone to help you through it, and get some experience for yourself.
System Overview
Rotary Encoders
There are three components to a digital setting circles system. First, rotary encoders must be mated to the two axes of the telescope’s mount. Rotary encoders are devices which measure rotational motion. Visually, they bear some resemblance to potentiometers, except that they have no stops (they are able to rotate continuously). Inside, the shaft of the rotary encoder has a clear plastic disk with alternating opaque lines and clear spaces between them, all around the periphery of the wheel. When the shaft and wheel turn, the movement of the opaque lines alternately blocks and unblocks the light path between two emitter/sensor pairs. This is translated into voltage pulses which indicate rotation of the shaft (low when the emitter/sensor pair is blocked by a line, high when not). The two emitter/sensor pairs are arranged such that when one sees the middle of a line, the other sees an edge of a line. The two emitter/sensor pairs are usually labeled as channels A and B.
If the encoder shaft is turned at a uniform speed in one direction, and the voltages from channels A and B are observed, the pattern in Figure 1 would be observed. Note that channel A leads channel B by one quarter of a full cycle (a full cycle is the time taken from when a pulse begins to when the next one begins).
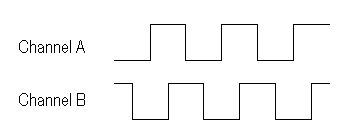
Figure 1. Example voltage output for rotary encoder turning in one direction.
Figure 2, on the other hand, shows the voltages when the encoder shaft turns in the opposite direction. Note that now channel A lags channel B by a quarter of a full cycle. Knowledge of the relationship between channels A and B allows the direction of rotation to be determined. Additionally, by counting the transitions of the pulses from both channels, we can improve the resolution obtained from the encoder. Knowing what we do about this quadrature mode of the encoder (that is, comparing both channels to determine direction), we can obtain a resolution of four times the stated cycles per revolution of the encoder. Thus, an encoder which has 1000 cycles per revolution can be used to measure rotation down to 1/4000th of a revolution. In this case, we say that the encoder has 4000 tics per revolution.
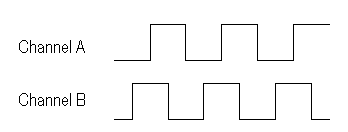
Figure 2. Voltage output for rotary encoder traveling in the opposite direction of that in Figure 1.
Decoder
Our second component, the decoder, is an electronic device which monitors the two channels of each of the two rotary encoders and keeps track of the relative angle of the encoder shaft. To do this, the decoder must know how many tics will occur per revolution of each axis on the telescope. If the rotary encoders are mounted directly to the axes of the telescope, then this number will be the same as the number of tics per revolution of the encoder (this is commonly the case for dobsonian scopes). If gears or pulleys are used to connect the encoders to the telescope, then the appropriate gear ratio must be used to compute the number of tics per revolution for each axis.
The decoder stores a single number for the position of each axis. If the number of tics per revolution for an axis is 4000, for example, this number might be stored in the range from 0 to 3999, or alternatively, in the range from -2000 to 1999. By taking that number, dividing it by 4000, and multiplying by 360 degrees, you can determine the relative angle for the axis. However, this is not a celestial angle. It is merely the angle between where the telescope was pointing at startup and where it points now. The next step is to convert each of these two angles into the celestial angles which indicate where the telescope is pointed.
Computer
The third component of our system is a computer. The job of the computer (which might be a PC, or it might be some special-purpose dedicated circuit) is to convert the relative angles from the decoder into absolute celestial angles. To do this requires the employment of a coordinate transformation algorithm. There are two coordinate systems in play here. The first is the system defined by the telescope axes and the angles returned by the decoder. The other coordinate system is the celestial coordinate system, defined by the positions of the stars. It is possible (see the “Astronomical Computing” column of the February 1989 issue of Sky and Telescope for further explanation) to mathematically define the relationship between the two coordinate systems if the coordinates of three positions are known in both systems. Thus, one of the activities when preparing your digital setting circles for an evening of observing is to perform an alignment. Commonly called a two star alignment, this process requires that you aim your telescope at two stars for which the coordinates are precisely known, and to tell the computer those coordinates (I said three positions were needed–the third is obtained by using the cross-product of the angles of the first two stars). The computer then computes the mathematical relationship between the two systems, and then uses that relationship to convert the encoder angles into celestial angles.
Stand-alone systems like the Orion’s Sky Wizard incorporate the decoder and the computer in one small box which contains a display and some buttons for user manipulation. Other types of systems use a decoder box which connects to a PC through the serial port, relying on the PC software to do the work of converting the angles. My system is of the second type. The circuit I describe below is the decoder box, and it connects to the serial port of your PC.
My Decoder Box Design
My decoder box design centers on the use of a PIC16F84 microcontroller chip from Microchip, Inc. This versatile chip is easy to program–the software development tools are available from Microchip for free, and the hardware programmer (the device which places the code into the chip itself) can itself be built cheaply and easily (and reused for other projects).
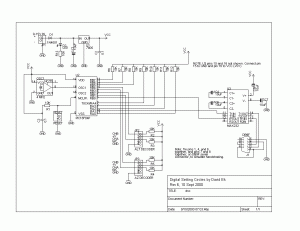
Here is the schematic diagram of the decoder box:
Some words about the design are warranted. Starting in the top left corner of the schematic is the voltage input and voltage regulation. U1 is a 7805 voltage regulator which supplies a regulated +5V DC output for the rest of the circuit. D1 is a polarity protection diode, to protect the rest of the circuit in case the battery is connected backwards. The battery itself should be able to supply +9 to +15V DC at at least 50 mA (I’ve used a 9V transistor battery and gotten a few hours of operation). You could also use a wall-wart type DC power supply with the appropriate voltage and current rating. D2 is an LED power-on indicator, and R13 serves to limit the current through D2. If you don’t want the power-on indicator, simply omit those two parts (and the corresponding ground connection, of course). Capacitors C1 and C2 help filter out any voltage ripple in the input.
U2 is the heart of the circuit–the PIC16F84 microcontroller. It performs two functions: monitoring the encoder channels and tracking encoder positions, and communicating the encoder positions to the PC. There are six data lines coming into U2, described in the table below. Two are for serial communications with the PC, and the other four are the A and B channels for the two encoders. U2 monitors the encoder channels, updates the encoder angles (which it stores internally), and listens for and responds to queries for the encoder angles from the PC. The PIC16F84 has to be loaded with a program for it to perform its function. This is detailed on the construction page.
| Pin Label | U2 Pin Number | Function |
|---|---|---|
| RB0 | 6 | Serial input from the PC |
| RA1 | 18 | Serial output to the PC |
| RB1 | 7 | Altitude encoder channel A |
| RB2 | 8 | Altitude encoder channel B |
| RB3 | 9 | Azimuth encoder channel A |
| RB4 | 10 | Azimuth encoder channel B |
The unused I/O pins on U2 are tied to +5V using 10K pullup resistors (R6 through R12). Power is applied to pin 14, and pin 5 is ground. Pin 4 is the reset pin, held high through 10K pullup resistor R1. The connector labeled RESET provides an easy way to short pin 4 to ground momentarily to reset U2 (restart its program) if necessary. C3 is an additional filter capacitor (to take out any voltage ripple).
OSC1 is a TTL oscillator which supplies U2 with a 4.0 MHz clock signal. The output of OSC1 goes to pin 16 of U2. The speed of OSC1 determines the speed at which the program in U2 will execute. U2 instructions execute at 1/4 the rate of OSC1 (in this case, 1 MHz). The speed of OSC1 must be 4 MHz for the device to work properly, as the timing for the serial communications is based upon a 1 MHz instruction time.
U3 is a MAX232 TTL-RS232 level converter. The serial communications pulses generated by and expected by U2 are at TTL levels (0V and +5V), while a PC expects RS232 levels (-12V and 12V). The MAX232 takes care of converting one to the other so that the PC and U2 each get the desired levels. Capacitors C4 through C7 are specified by the MAX232 data sheet, although I don’t know exactly what their functions are. J1 is the DB9F serial connector for a serial cable connected to a PC serial port. Note that some of the pins on J1 are connected to each other. This is to simulate serial handshaking if the serial port on the PC requires it.
JP2 and JP3 are the connectors for the two encoders. There are 10K pullup resistors on channels A and B of both encoders (these are R2 through R5). You might notice that I connected pins 4 and 5 on each connector. This is so that I can use a four-pin connector instead of a five-pin connector if I desire, since pin 4 is not used. That way, I get ground from pin 4 instead of pin 5. Shorting pins 4 and 5 on each connector has no effect if you’d rather use five-pin connectors, though.
Communications Protocol
The interface communicates with the PC through one of several predetermined protocols. I’ve implemented protocols for BBox, NGC-MAX (which is also SGT-MAX and a few others), and MicroGuider III. Each of these protocols requires the interface to wait for a command from the PC via the serial port, and to return information (such as the current encoder positions or interface status) based upon the command received. In other words, the interface doesn’t speak until spoken to.
Besides the other interface types I’ve mentioned above, I also implemented my own protocol for communications. Here’s the protocol I implemented. Note that everything is byte-oriented. A, B, C, and D are always single bytes (hence the usage of low byte and high byte).
| Received | Reply | Description |
|---|---|---|
| zABCD | r | Set the encoder resolution (ticks per axis revolution):
A = declination resolution low byte |
| h | ABCD | Report the encoder resolution (ticks per axis revolution):
A = declination resolution low byte |
| y | ABCD | Report the encoder positions (range from zero to [resolution-1]):
A = declination position low byte |
| p | A | Report the number of encoder errors and reset the counter to zero:
A = number of encoder errors |
Construction
My construction page covers the building of this interface.